Korrelationen

Korrelationen sind ein Maß für den statistischen Zusammenhang zweier Datenreihen. Ein Korrelationsmaß impliziert daher auch stochastische Abhängigkeit - ohne jedoch auf kausale Zusammenhänge schließen zu können.

Korrelationen werden i.A. der deskriptiven Statistik zugeordnet. Durch eine Reihe von Verfahren, wie z.B. partielle Korrelation, multiple Korrelation oder Faktorenanalyse, kann die einfache Korrelation zweier Variablen auf Beziehungen zwischen zwei Variablen unter Berücksichtigung des Einflusses weiterer Variablen werden.

Korrelationen sind ein unverzichtbares Werkzeug für viele Forschungsgebiete und stehen häufig am Beginn jeder weiteren Datenanalyse, wie z.B.:

• multiple Regression
• Faktorenanalyse
• Clusteranalyse
• Mediator- und Moderator-Analyse

Pearson Produkt Moment Korrelation

Die häufigst verwendete Form der Korrelationsberechnung ist die Pearson-Produkt-Moment Korrelation. Bei dieser Methode wird die Beziehung zwischen zwei metrische Variablen (bzw. eine metrische und eine dichotome Variable) als Kennzahl mit dem Wertebereich \(r \in [-1,1]\) berechnet.

Die Berechnung einer Korrelation ist für sich gesehen an keine Voraussetzungen gebunden. Hingegen fordern eine sinnvolle Interpretationen der berechneten Kennwerte und vor allem die statistischen Tests von Korrelationskoeffizienten folgende inhaltliche und formale Überlegungen:

• Skalenniveau: der Korrelationskoeffizient liefert sinnvoll interpretierbare Ergebnisse wenn die Variablen mindestens intervallskaliert sind (oder für eine intervallskalierte und eine dichotome Variable¹).

• Endliche Varianz (und Kovarianz): bei Erhöhung des Stichprobenumfangs darf sich die Variabilität nicht immer weiter erhöhen, sondern sollte sich stabilisieren. Bei Variablen, die bivariat normalverteilt sind, ist diese Voraussetzung automatisch gegeben. Der Korrelationskoeffizient ist damit auch gleichzeitig der Maximum-Likelyhood Schäzter des Korrelationskoeffizienten in der Grundgesamtheit (asymptotisch erwartungstreu und effizient).

Abbildung 5: Endliche Varianz²

• Linearität: die Korrelation ist ein Maß für lineare Abhängigkeit. Abweichungen der Daten von dieser Linearitätsannahme führen zu einer mehr oder weniger starken Verzerrung des Korrelationskoeffizienten, wie in den nachfolgenden Beispielen gezeigt wird:

Abbildung 6: Linearität und Korrelation

Vor allem zur Prüfung der Signifikanz einer Korrelation sollem man weitere Voraussetzungen überprüfen:

• Normalverteilung: Korrelation berechnen sich aus dem Kreuzprodukt von z-standardisierten Werten zweier Variablen. Für diese Berechnung wird der Mittelwert als zentraler Kennwert verwendet, welcher nur dann ein “sinnvoller” Kennwert für die Daten ist, wenn diese zumindest symmetrisch und im besten Fall normalverteilt sind.

• Homoskedastizität: bedeutet gleichmäßige Streuung der Daten zweier (exogene und endogene) Variablen. Sind die exogene und die endogene Variable³ nicht mehr identisch verteilt, d.h. sie ändern ihre Variablität mit zu/abnehmenden Werten einer Variablen, spricht man von Herteroskedastizität. Das hat zur Folge hat, dass die KQ⁴-Schätzer nicht mehr effizient sind und der Standardfehler der Koeffizienten verzerrt und nicht konsistent wird.

Abbildung 7: Variablität(einschränkung) und Korrelation

• KEINE Ausreißer: der Korrelationskoeffizient ist nicht robust gegenüber Ausreißern. Dies bedeutet, dass Ausreißer den Korrelationskoeffizienten sowohl künstlich erhöhen als auch künstlich senken können.

Abbildung 8: Einfluss von Ausreißer bei linearer Modellbildung

• KEINE Kluster: es kann vorkommen, dass zwei oder mehr Gruppen eine Korrelation zeigen, die eigentlich getrennt untersucht werden müssten. Dieses Problem wird oft auch mittels partieller Korrelation umgangen, bei der mögliche Drittvariablen statistisch konstant gehalten werden.

Abbildung 9: Kluster und deren Auswirkung bei linearer Modellierung

Beispiel Pearson Korrelation

Im folgenden, fiktiven Beispiel werden die Zusammenhänge von Klausurperformanz (EP), Intelligenz (IQ), Vorbereitungszeit (VZ) und Prüfungsangst (PA) korreliert. Der Code zum Laden der Daten sowie die Daten selbst sind in nachfolgender Ausgabe/Tabelle dargestellt:

    load("Daten/CorrBsp1.Rda")

EP	IQ	VZ	PA
74	109	16	117
67	96	18	122
72	106	13	108
66	89	12	97
63	93	14	98
67	102	15	106

Aufgabe 1

Kopiere den obigen Code zum Laden der Daten in eine R-Script-Datei. Führen nun folgende Aufgaben aus:

1. Ermittle mit einer geeigneten Funktion die Korrelationen und prüfe diese auch auf statistische Signifikanz.
2. Zeichne einen Korrelationsplot mit dem Paket corrplot.
3. Berechne die Teststärke der Korrelation \(r(IQ, EP)\) (Hinweis: verwende die Funktion pwr.r.test des Pakets pwr).
4. Verwende diese Funktion (pwr.r.test) um für eine Korrelation \(r(x,y) = 0.21\) den optimalen Stichprobenumfang zu berechnen.
5. Prüfe mit Hilfe der Funktion mvn aus dem Paket MVN die Voraussetzung der bivariaten Normalverteilung der Variablenpaare (EP,IQ), (EP, VZ) und (EP,PA).
6. Berechne die durchschnittliche Korrelation von \(r_1(EP,IQ)\), \(r_1(EP,VZ)\) und \(r_1(EP,PA)\). Beachte, dass zur Berechnung von durchschnittlichen Korrelationswerten eine Fisher-Z-Transformation notwendig ist (Hinweis: verwende die fisherz() und fisherz2r() des Pakets psych).
7. Prüfe, ob der Unterschied der Korrelationskoeffizienten \(r(EP,IQ) = 0.47\) und \(r(EP,VZ) = 0.36\) statistisch signifikant ist. Verwende die Funktion paired.r() aus dem Paket psych.

Lösung Aufgabe 1

Kausalität

Eine relevante (statistisch signifikante) Korrelation liefert keinen Beleg für die Kausalität. Vor allem in der Medizin und Psychologie suchen Forscher nach Kriterien für Kausalität. Es existieren mehrere Ansätze zur Erklärung der Ursächlichkeit einer Korrelation (siehe z.B. die 9 Bradford-Hill-Kriterien).

Partial- Semipartialkorrelation

Die partielle Korrelation ist die bivariate Korrelation zweier Variablen, welche mittels linearer Regression vom Einfluss einer Drittvariablen bereinigt wurden.

Eine Semipartialkorrelation ist ein Zusammenhang zwischen einer residualisierten und einer nicht-residualisierten Variable.

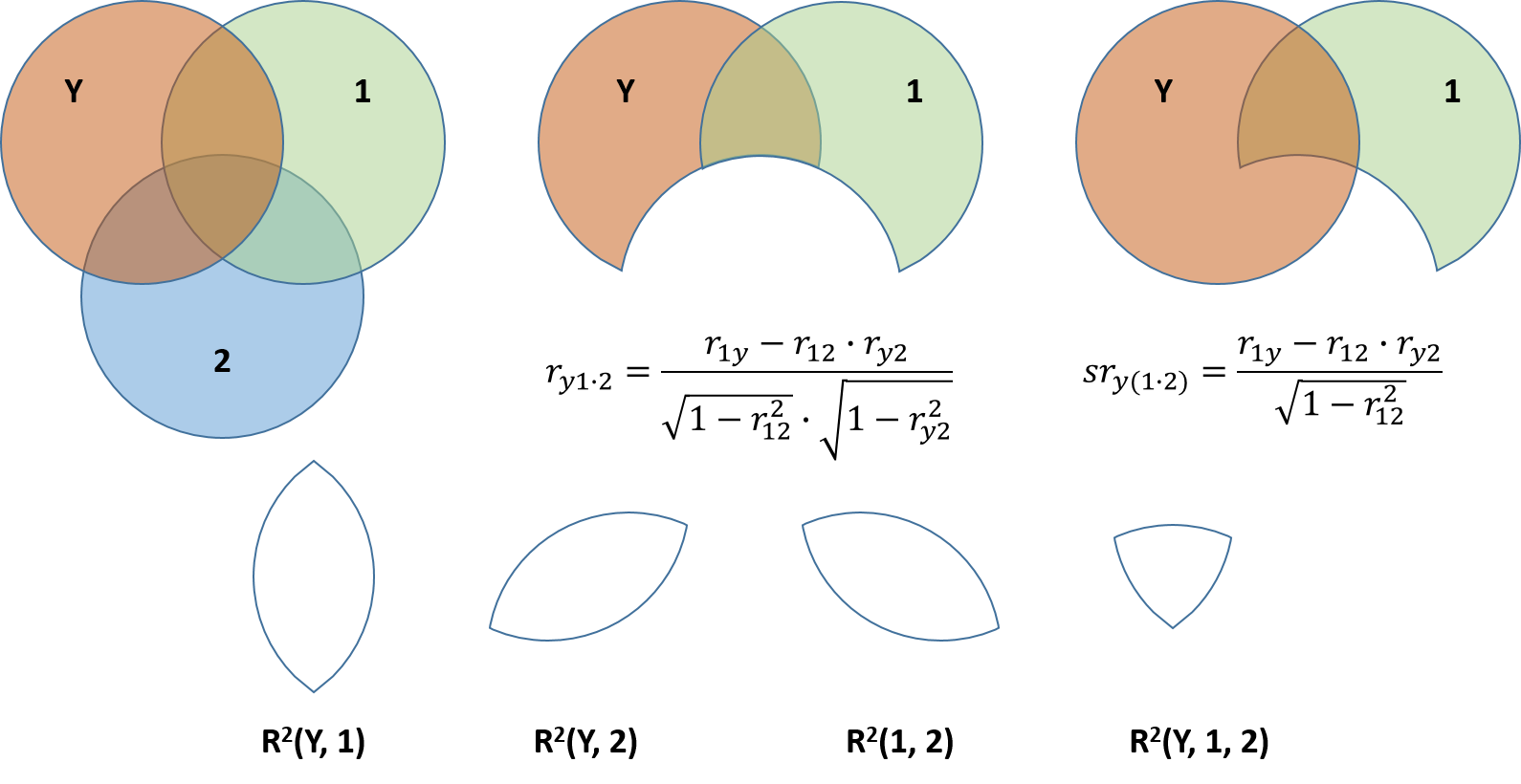
Abbildung 10: Partial und Semipartialkorrelation in einem Venn-Diagramm dargestellt

Beispiel Partial- Semipartialkorrelation

Folgendes Beispiel verdeutlicht die Wirkungsweise einer Partial- und Semipartialkorrelation. Kopier den folgenden Code in ein R-Script und führe diesen dann aus. Diskutiere die Ergebnisse.

    examData  <- read.delim("Daten/Exam Anxiety.dat", header = TRUE)
    examData2 <- examData[, c("Exam", "Anxiety", "Revise")]
    
    # Normale Korrelation
      pander::pander(round(cor(examData2),2))
    # Partielle Korrelation
      # library(ppcor)
      pander::pander(round(ppcor::pcor(examData2)$estimate,2))
    # Partialkorrelation mit Linearen Modell    
      Mod1            <- lm(Exam ~ Revise, data = examData2)
      Res_Exam_Rev    <- residuals(Mod1)    
      Mod2            <- lm(Anxiety ~ Revise, data = examData2)
      Res_Anx_Rev     <- residuals(Mod2)    
      pr_Exam_Anx_Rev <- round(cor(Res_Exam_Rev, Res_Anx_Rev), 2)

In diesem Code wurde zur Veranschaulichung der Wirkungsweise einer Partial/Semipartialkorrelation eine lineare Regression verwendet. Was dabei genau passiert sei durch nachfolgende Abbildung nochmals veranschaulicht:

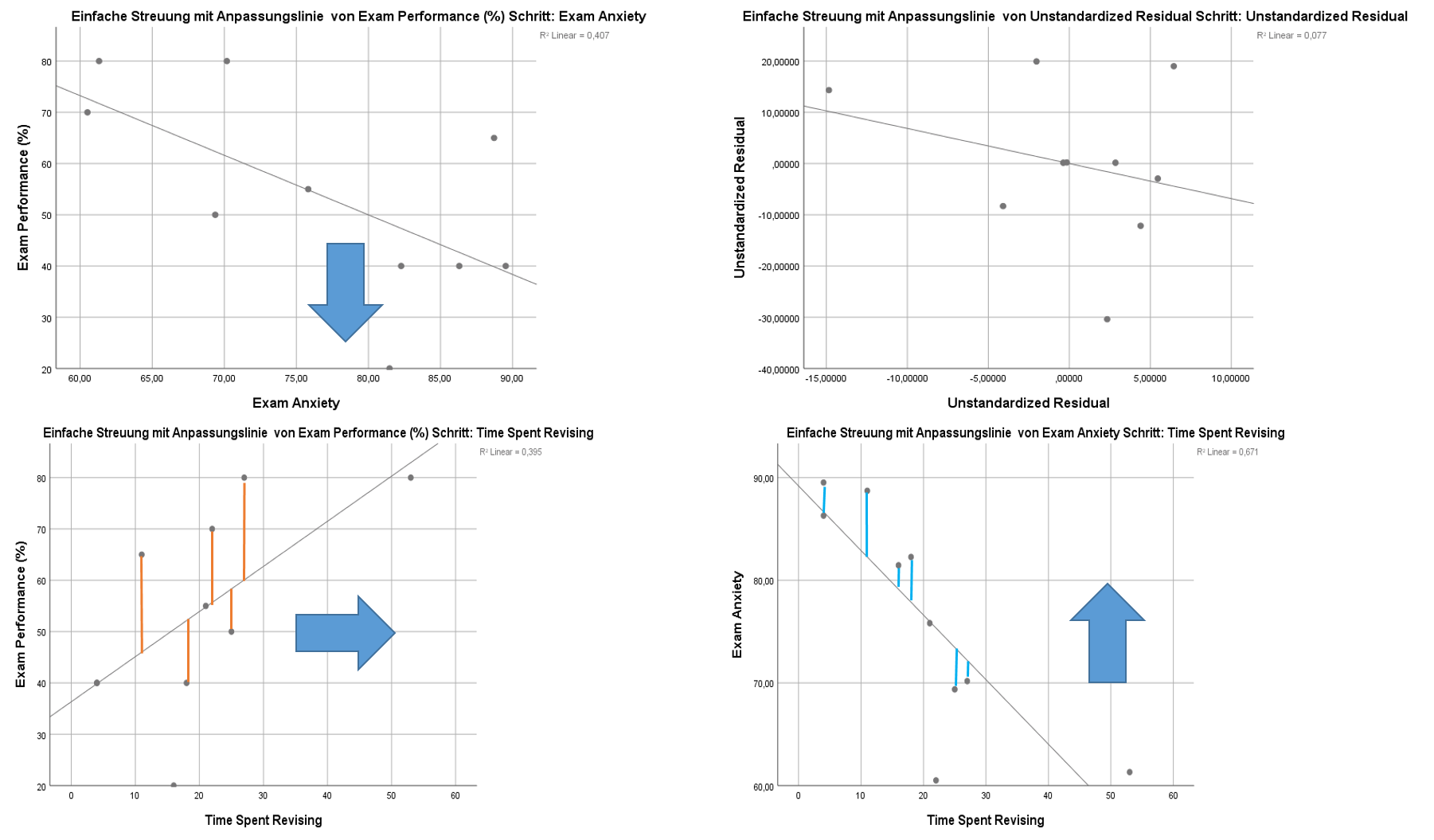
Abbildung 11: Partialkorrelation als lineares Regressionsmodell. Für die Beziehung Examperformance und Exam Anxiety soll der Effekt von Revisiotime berücksichtigt werden. Die roten Linien entsprechen den Residuen der Regression Revisiontime mit Exam Performance. Die blauen den Residuen der Regression Revisiontime mit Exam Anxiety. Der linke obere Graph stellt die Beziehung von Anxiety und Examperfomance bereinigt von Revisiontime dar. Details siehe nachfolgendemn Text.

1. Examperformance wird durch Revisiontime vorhergesagt. Die Residuen sind jener Anteil an Variabilität der Examperformanz, der nicht durch Revsiontime vorhergesagt werden können⁵. Diese über die durch Revisiontime erklärbare Variabilität von Examperformance kann zurückgeführt werden auf:
   • andere erklärende Merkmale, bzw.
   • Messfehler
2. Anxiety wird durch Revisiontime vorhergesagt. Auch hier gilt wieder, dass die Residuen der Variabilität von Anxiete, bereinigt von Revisiontime entsprechen.
3. Die Korrelation der Residuen entspricht nun genau der Partialkorrelation \(r_{Y1\cdot2}\)

Bei der Semipartialkorrelation bereinigt man nun nicht beide Variablen, sonder eben nur einen Teil (z.B. wird nur die Anxiety von Revisiontime bereiningt).

Kopiere den nachfolgenden Code in ein R-Script und führe diesen aus. Diskutiere die Ergebnisse!

    # Semipartielle Korrelation
      pander::pander(round(ppcor::spcor(examData2)$estimate,2))
    # Semipartialkorrelation mit Linearen Modell    
      sr_Exam_Anx_Rev <- round(cor(examData2$Exam, Res_Anx_Rev), 2)

Korrelationstechniken

Neben dem Pearson-Produkt-Moment-Korrelationskoeffizienten \(r\) existieren noch etliche weitere Korrelationskoeffizienten und Zusammenhangsmaße. Die meisten hiervon sind Sonderfälle der Pearson-Produkt-Moment-Korrelation. Nachfolgende Tabelle zeigt, wann welcher Koeffizient berechnet werden soll. Die Verwendung unterschiedlicher Korrelationsberechnungen ist i.A. abhängig vom Skalenniveau der beteiligten Variablen.

Abbildung 12: verschiedene Korrelationskoeffizienten

Spearman und Kendall

Für die Berechnung des Pearson-Korrelationskoeffizienten (\(r\)) ist das Vorliegen von kontinuierlichen Variablen erforderlich. Bei ordinalskalierten Daten wird eine der folgenden Rangkorrelation berechnet:

1. Spearman \(r_s\): Spearman-Rangkorrelation setzt voraus, dass Ränge gleichabständig sind⁶ und keine Ausreißer vorliegen.
2. Kendall \(\tau\): Ränge müssen nicht gleichabständig sein und Ausreißer beeinflussen diesen Korrelationskoeffizienten weit weniger als z.B. den den \(r_s\).

Bei den Kendall-Koeffizienten unterscheidet man noch drei unterschiedliche Maße⁷:

• Kendalls \(\tau_a\): Rangbindungen werden nicht berücksichtigt.
• Kendalls \(\tau_b\): Rangbindungen werden berücksichtigt.
• Kendalls \(\tau_c\): für nicht quadratische Kontingeztafeln.

Zur Veranschaulichung der verschiedenen rangbasierten Korrelationsmaße sind folgende Aufgaben zu bearbeiten:

1. Berechne zuerst nochmal die Pearson-Korrelation \(r(EP,IQ)\) des bereits geladenen Datensatzes und rechne dann eine Spearman Korrelation. Verwende nun die Funktion cor() des Basispakets. Vergleiche die Ergebnisse!
2. Vererwende die Funktion rank() um den Variablen EP und IQ Ränge zuzuordnen. Speichere die Ergebnisse in EP_Ranks und IQ_Ranks und berechnen Sie anschließend eine Pearson-Korrelation. Vergleiche die Ergebnisse mit dem vorherigen Pearson-\(r\).

Lösung Aufgabe 2

Biseriale Korrelation

Biseriale Korrelationen kommen zur Anwendung, wenn ein Merkmal Intervall- oder Ordinalskaliert und das zweite Merkmal dichotom Nominalskaliert ist. Für das Nominalskalierte Merkmal unterscheidet man noch zwischen:

• Echt dichotome Variable: natürlich vorkommende Gruppenteilung wie z.B. wahr/falsch, männlich/weiblich, etc. Der Zusammenhang einer solchen mit einer intervallskalierten Variablen wird durch die punktbiseriale Korrelation beschrieben.
• Künstlich dichotome Variable: wird eine kontinuierliche Variable in zwei Gruppen aufgeteilt, wie z.B. zwei Altersgruppen (jung, alt), oder hohe Leistungsfähigkeit vs. niedrige Leistungsfähigkeit, etc., dann spricht man von einer künstlich dichotomen Variablen. Zusammenhänge dieser mit einer intervallskalierten Variablen werden durch die biseriale Korrelation beschrieben.

Kopier den folgenden Code in dein R-Script und bearbeite folgende Aufgabenstellungen:

1. Verwende die Funktion dicho() des Pakets sjmisc um alle Variablen über den Median zu dichotomisieren (Hinweise: ersetze die XXX im Code mit den entsprechenden Werten).
2. Berechne die biseriale Korrelation der Variablen IQ und der Exam-Performance-Gruppe (EP_Grp).

      # Zuerst wird die Examensperformanz über den Median in zwei Gruppen geteilt
      # library(sjmisc)
      DF_Biserial <- DF_Korr[order(EP), ]
      DF_Biserial <- sjmisc::dicho(XXX,
                                   dich.by = "XXX", 
                                   as.num = FALSE, 
                                   var.label = "Grp",
                                   val.labels = c("low", "high"), 
                                   append = TRUE, 
                                   suffix = "_Grp")

      biserial(x = XXX, y = XXX)

Phi-Koeffizient

Korrelationen zwischen echt-dichotomen Variablen (männlich/weiblich, etc.) können mit dem Phi-Koeffizienten berechnet werden. Um den Phi-Koeffizienten zu berechnen, werden Häufigkeiten in Form einer Vier-Felder-Tafel benötigt.

Abbildung 13: Beispiel und Berechnung des Phi-Koeffizienten

Folgendes einfaches Beispiel zeigt die Berechnung des Phi-Koeffizienten sowie dessen Äquivalenz mit einer Pearson-Korrelation:

      Geschlecht <- c(1,  1,  0,  0,  1,  0,  1,  1,  1)
      Bestanden  <- c(1,  1,  1,  0,  0,  0,  1,  1,  1)
      
      VFT        <- table(Geschlecht, Bestanden)
      pander::pander(VFT)
      
      cor(Geschlecht, Bestanden)
      
      phi(VFT)
      CST <- chisq.test(VFT, correct = FALSE)
      pander::pander(CST)
      qchisq(p=.95,df=1) # kritischer Chi-Square-Wert bei einem Freiheitsgrad und Alpha = 5%

Die Anzahl der Freiheitsgrade beträgt in diesem Fall immer eins, da wir es mit zwei dichotomen Merkmalen zu tun haben.

Tetrachorische Korrelation

Soll der Zusammenhang zwischen zwei künstlich-dichotomen Variablen berechnet werden, die aus stetigen, normalverteilten latente Variablen abgeleitet wurden (z.B. Intelligenz und Examperformanz in Statistik), verwendet man die tetrachorische Korrelation.

Auf Details zur Berechnung der Kenngröße wird hier verzichtet. Grundlage ist wiederum eine Vier-Felder-Tafel (wie beim Phi-Koeffizienten), wobei die tetrachorische Korrelation nicht so stark von der Randverteilung der Vier-Felder-Tafel abhängt. Zu beachten ist jedoch, dass die Zellbesetzung von b und c nicht 0 sein darf! Nachfolgendes Beispiel sollte die Anwendung der tetrachorischen Korrelation verdeutlichen. Lade dazu den folgenden Code und führe diesen Zeilenweise aus. Diskutiere die Ergebnisse!

      # library (psych) 
      load("Daten/TetraCorrBsp.Rda")
      TCC_Res <- tetrachoric(DF_TCC)
      pander(TCC_Res$rho)

Polychorische Korrelation

Um Korrelationen zwischen ordinalen Daten zu beschreiben, verwendet man die polychorische Korrelation. Dabei schätzt man die Korrelation zwischen zwei (ordinalen) Merkmalen, die in mehr als zwei geordnete Kategorien unterteilt sind. Die Berechnung ist überaus komplex und wird hier nicht dargestellt.

Polychorische Korrelationen werden unter anderem verwendet, um konfirmatorische Faktorenanalysen mit ordinalen Daten zu berechnen. Es ist mit Programmen wie R, AMOS, LISREL oder MPlus auch möglich, exploratorische Faktorenanalysen mit polychorischen Korrelationen durchzuführen.

---

1. dieser Spezialfall ist unter biserialer, bzw. punktbiserialer Korrelation bekannt.↩

2. die Abbildungen wurden der Website Matheguru entnommen↩

3. eine exogene Variable ist eine erklärende Variable, die mit der Störgröße unkorreliert ist (sogenannte Exogenität). Eine endogene Variable in einem multiplen Regressionsmodell ist eine erklärende Variable, die entweder aufgrund einer ausgelassenen Variablen, eines Messfehlers oder wegen Simulatanität mit der Störgröße korreliert ist (sogenannte Endogenität).↩

4. KQ steht für kleinste Quadrate (auch MLS - Minimum Least Square, oder OLS - Ordinary Least Square) und ist eine einfache Schätzung über minimierte quadradische Abstände der Residuen (Fehler) zu einem Modell (Mittelwert, Gerade, etc.)↩

5. anderenfalls würden ja alle beobachteten Werte auf der Gerade liegen!↩

6. diese Voraussetzung ist eher selten erfüllt. Sie ist gleichzusetzen mit der Annahme, dass in einem Skirennen der erste, zweite, dritte, etc. Platz genaus die gleichen Zeitabstände aufweisen. Ist diese nicht gegeben, sollte Kendalls \(\tau\) verwendet werden.↩

7. Details zu den unterschiedlichen Kendalls-\(\tau\) sind der Literatur zu entnehmen. Weitere Betrachtungen beziehen sich auf das Kendalls-\(\tau_b\)↩