Multiple Regression
Regressionsanalysen sind statistische Analyseverfahren, die zum Ziel haben, Beziehungen zwischen einer abhängigen und einer oder mehreren unabhängigen Variablen zu modellieren. Sie werden insbesondere verwendet, wenn Zusammenhänge quantitativ zu beschreiben oder Werte der abhängigen Variablen zu prognostizieren sind.
In der Statistik ist die multiple lineare Regression (auch mehrfache lineare Regression (MLR) oder lineare Mehrfachregression genannt), ein Spezialfall des allgemeinen Konzepts der Regressionsanalyse.
Die Multiple lineare Regression ist ein statistisches Verfahren, mit dem versucht wird, eine beobachtete abhängige Variable durch mehrere unabhängige Variablen zu erklären. Die multiple lineare Regression stellt eine Verallgemeinerung der einfachen linearen Regression dar. Das Beiwort „linear“ bedeutet, dass die abhängige Variable als eine Linearkombination (nicht notwendigerweise) linearer Funktionen der unabhängigen Variablen modelliert wird (siehe Wikipedia).
Definition
Die formale Definition eines multiplen linearen Modells ist:
\[\begin{equation} y_i = b_0 + b_1 \cdot x_{1i} + \cdots + b_k \cdot x_{ki} + \varepsilon_i \tag{1} \end{equation}\]
Die wesentlichen Parameter dieses Modells sind:
- Intercept \(b_0\): jener Wert den \(y_i\) einnimmt, wenn \(x_{ji} = 0\) ist (mit \(i \in [1,N]\), \(N=\) Anzahl der Beobachtungen und \(j \in [1,k]\), \(k=\) Anzahl der Prädiktoren).
- Steigung \(b_i\): die Zunahme von \(y_i\), wenn \(x_{ji}\) sich um eine Einheit erhöht, bei gleichzeitigem Konstanthalten der restlichen Prädiktorwerte \(x_{mi}\) (mit \(m [1,k]\) und \(m \ne j\))!
Des Weiteren berücksichtigt dieses Modell einen Fehler (\(\varepsilon_i\)). Betrachtet man das multiple Modell isoliert (also ohne Fehlerterm), ist folgende Schreibweise üblich:
\[\begin{equation} \hat{y}_i = b_0 + b_1 \cdot x_{1i} + \cdots + b_k \cdot x_{ki} \tag{2} \end{equation}\]
Zur Veranschaulichung betrachten wir anhand der folgenden Beispieldaten folgendes Modell mit zwei Prädiktoren:
\[\begin{eqnarray*} \hat{wage}_i = b_0 + b_1 \cdot educ_{i} + b_2 \cdot exper_{i} \tag{3} \end{eqnarray*}\]
Es sollte als das Einkommen (\(wage_i\)) durch den Ausbildungsstand (\(educ_i\)) und die Arbeitserfahrung (\(exper_i\)) vorhergesagt werden. Die verwendeten Daten stammen vom Paket DAAG (Data from the 1985 Current Population Survey) und werden als Datenframe (CPS85) automatisch mit dem Laden des Pakets zur Verfügung gestellt. Erstelle ein neues R-Script, in welches in den ersten Zeilen der Anfangs erwähnte Codeteil zum Laden der Pakete kopiert werden soll. Anschließend kopier den nachfolgenden Code und führe diesen aus.
# library(mosaicData) fuer CPS85
model_1 <- lm(wage ~ educ, data = CPS85)
model_2 <- lm(wage ~ educ + exper, data = CPS85)
Det_model_2 <- pander::pander(summary(model_2))
rockchalk::plotPlane(model = model_2, plotx1 = "educ", plotx2 = "exper")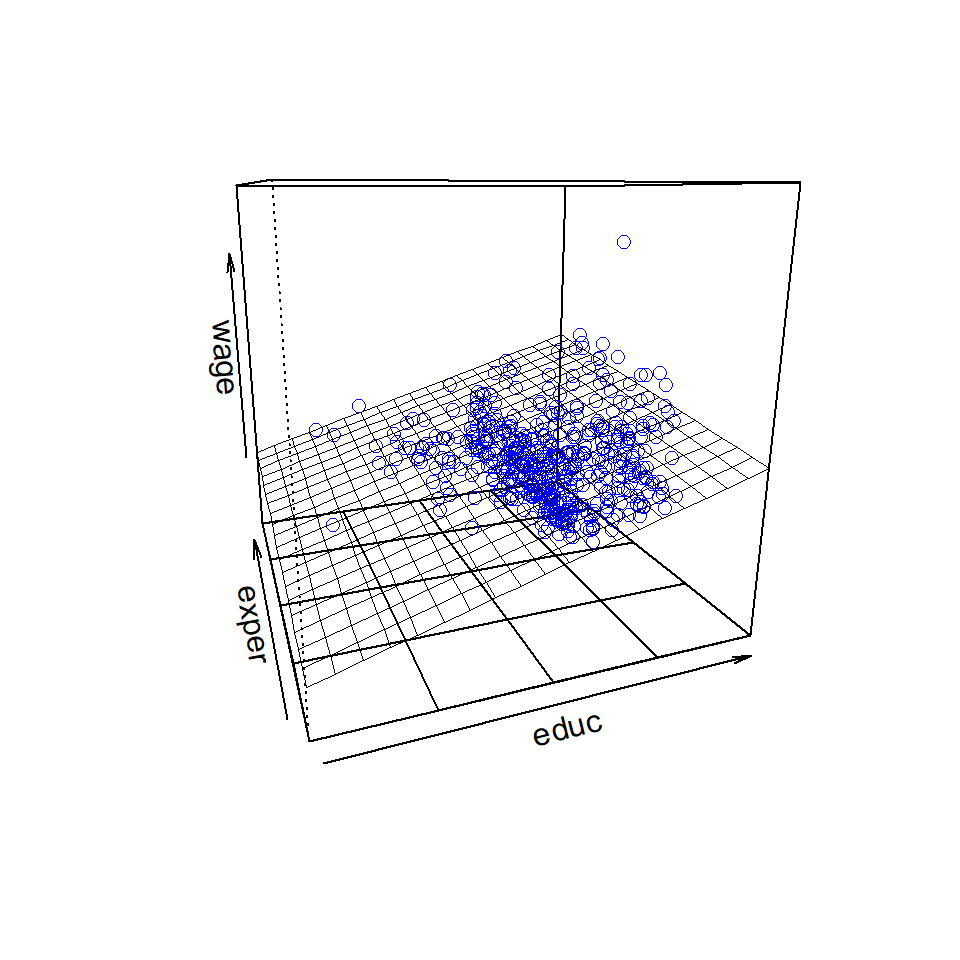
Der Koeffizient \(b_2\) entspricht der Zunahme des Gehaltes \(\hat{y}_i\) wenn sich die Erfahrung \(x_{2i}\) um eine Einheit erhöht und die Ausbildung \(x_{1i}\) konstant gehalten wird. In nachfolgernder Tabelle sind die Werte der Vorhersagen des Modells für den vorliegenden Datensatz auszugsweise dargestellt (übernimm den Code in dein R-Script und führe diesen aus):
MinExp <- min(CPS85$exper)
MaxExp <- max(CPS85$exper)
RowSeq <- seq(from = 1, to = MaxExp, by = 1)
educVon <- 10
educBis <- 18
AnzCols <- educBis - educVon + 1
Predicted <- matrix(NA, nrow = MaxExp, ncol = AnzCols)
for (i in seq(from = 1, to = MaxExp, by = 1)) {
new_input <- data.frame(educ = educVon:educBis, exper = i)
Predicted[i,] <- predict(model_2, newdata = new_input)
}
Predicted <- data.frame(seq(from = 1, to = MaxExp, by = 1), Predicted)
colnames(Predicted) <- c("Exp", "Edu10", "Edu11","Edu12", "Edu13",
"Edu14","Edu15", "Edu16","Edu17", "Edu18")
TabRows2Disp <- c(1:3, 53:55)
Predicted2Disp <- Predicted[TabRows2Disp,]
row.names(Predicted2Disp) <- NULL
pander::pander(Predicted2Disp, style = "rmarkdown")| Exp | Edu10 | Edu11 | Edu12 | Edu13 | Edu14 | Edu15 | Edu16 | Edu17 | Edu18 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 4.46 | 5.386 | 6.312 | 7.238 | 8.164 | 9.09 | 10.02 | 10.94 | 11.87 |
| 2 | 4.565 | 5.491 | 6.417 | 7.343 | 8.269 | 9.195 | 10.12 | 11.05 | 11.97 |
| 3 | 4.671 | 5.597 | 6.522 | 7.448 | 8.374 | 9.3 | 10.23 | 11.15 | 12.08 |
| 53 | 9.927 | 10.85 | 11.78 | 12.71 | 13.63 | 14.56 | 15.48 | 16.41 | 17.33 |
| 54 | 10.03 | 10.96 | 11.88 | 12.81 | 13.74 | 14.66 | 15.59 | 16.51 | 17.44 |
| 55 | 10.14 | 11.06 | 11.99 | 12.92 | 13.84 | 14.77 | 15.69 | 16.62 | 17.55 |
# library(reshape2) fuer melt
# library(ggplot) fuer Plots
CPS852Disp <- reshape2::melt(Predicted,
id.vars = "Exp",
measure.vars = c("Edu10", "Edu11", "Edu12",
"Edu13", "Edu14","Edu15",
"Edu16", "Edu17", "Edu18"))
CPS852Disp$Exp <- rep(1:55, 9)
colnames(CPS852Disp) <- c("Exp", "Edu", "WagePred")
p <- ggplot(CPS852Disp, aes(x = Exp, y = WagePred, color = Edu)) +
geom_line() +
theme_bw()
print(p, comment = FALSE)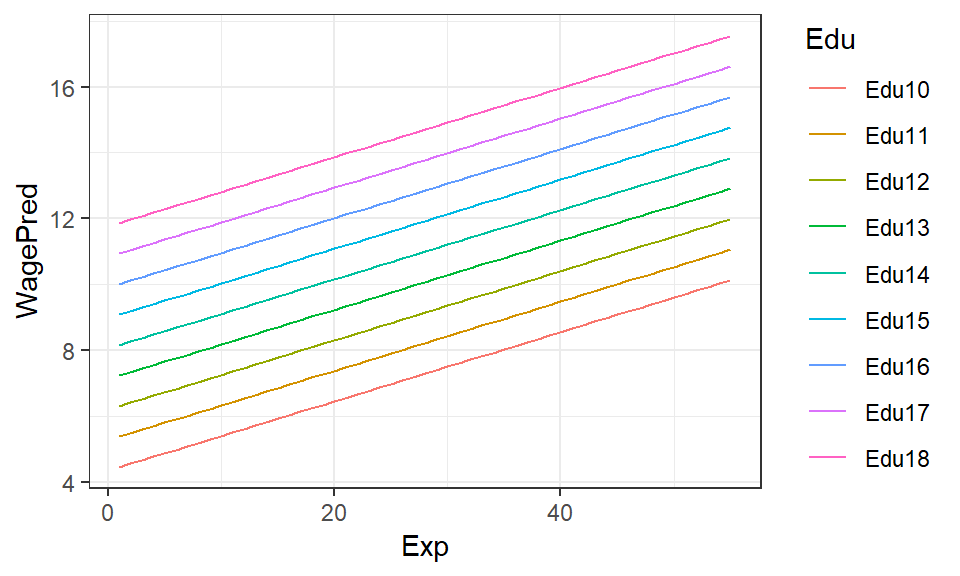
Modellvergleich
Ein Modell sollte die Wirklichkeit mit wenigen Parametern, aber in bestmöglicher Genauigkeit abbilden. Bei der Erstellung eines Modells werden aufgrund einer Stichprobe aus der Grundgesamtheit die Modellparameter (\(b\)’s) bestimmt. Um festzustellen, inwieweit ein Modell brauchbare Vorhersagen liefert, sollte man das Modell evaluieren. In den vorangegangen Beispielen wurden zwei Modelle (model_1 und model_2) erstellt.
Der Vergleich der Modelle ist über den Fehler (Residuen) des jeweiligen Modells möglich. Je kleiner der Fehler, desto besser bildet das Modell die beobachteten Werte ab. Im Idealfall (\(\varepsilon = 0\)), würden alle beobachteten Werte gleich den vorhergesagten Werten sein und damit auf der Linie liegen.
M <- data.frame(wage = CPS85$wage, educ = CPS85$educ, exper = CPS85$exper)
MV_Data <- data.frame(educ = M$educ, exper = M$exper)
MSE_Model1 <- round(mean(resid(model_1)^2),2)
# MSE_Model1 <- mean((M$wage - predict(model_1, newdata = MV_Data))^2)
StdResid <- rstandard(model_1)
# StdResid <- (resid(model_1)-mean(resid(model_1)))/sd(resid(model_1))
MSE_Model2 <- round(mean((M$wage - predict(model_2, newdata = MV_Data))^2),2)Der Modellvergleich der obigen Beispiele ergibt für das Modell 1 einen \(MSE_1 =\) 22.52 und für Modell 2 einen \(MSE_2 =\) 21.04.
Bei diesen Ergebnis lässt sich zunächst nur feststellen, dass der \(MSE_2\) kleiner als der \(MSE_1\) ist. Ob diese Verringerung des \(MSE\) von statistischer und/oder praktischer Signifikanz ist, wird im folgenden noch genauer betrachtet.
Mit einer einfachen ANOVA lässt sich nun auch die statistische Signifikanz der Änderungen im Fehler bei den verwendeten Modellen berechnen. Betrachten wir zunächst die statistische Änderung die Modell 1 im Vergleich zum Mittelwertsmodell erzielt:
# ANOVA Tests auf signifikante Aenderungen model_1 vs Mittelwertsmodell
# Berechnung der Quadratsummen fuer die Regression (educ)
preds_1 <- predict(model_1, newdata = CPS85)
AnzPred <- 2 # b_0 und b_1
SS_Regression_1 <- sum((preds_1 - mean(preds_1))^2)
Zdf_Regression_1 <- AnzPred - 1
MSS_Regression_1 <- round(SS_Regression_1 / Zdf_Regression_1, 2)
# Berechnung der Quadratsummen des Fehlers (Residuals)
Residuals_1 <- CPS85$wage - preds_1
SS_Residuals_1 <- sum(Residuals_1^2)
Ndf_Residuals_1 <- nrow(CPS85) - AnzPred
MSS_Residuals_1 <- round(SS_Residuals_1 / Ndf_Residuals_1, 2)
# Berechnung der Teststatistik
F_Wert <- round(MSS_Regression_1 / MSS_Residuals_1, 2)
# Berechnung der totalen Quadratsumme
SS_Total_1 <- sum((CPS85$wage - mean(CPS85$wage))^2)
CPS85_Total <- nrow(CPS85) - 1
# Vergleich mit den Ergebnissen der ANOVA
pander::pander(anova(model_1))| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| educ | 1 | 2053 | 2053 | 90.85 | 5.474e-20 |
| Residuals | 532 | 12023 | 22.6 | NA | NA |
Das Ergebnis zeigt uns, dass Modell 1 im Vergleich zum Mittelwertsmodell zu einer statistisch signifikanten Fehlerreduktion führt. Bei der händischen Berechnung der Prüfgrößen erhalten wir für die mittlere Quadratsumme der Regression (also der Varianz der Werte die durch das Modell vorhergesagt werden) einen Wert von \(MSS_{Regression} =\) 2053.29, welcher ident mit dem Wert der ANOVA-Tabelle ist.
Die restlichen Kennwerte stimmen auch mit dem Ergebnis der ANOVA überein (\(MSS_{Residual} =\) 22.6, F(1,532) = 90.85).
Wird das Modell 1 erweitert (auf Modell 2), stellt sich die Frage, ob diese Erweiterung im statistischen Sinn zu einer signifikanten Verbesserung führt. Bei diesem Vergleich wird nun die Änderung (Change Statistic) zwischen Modell 1 und Modell 2 auf Signifikanz geprüft.
# ANOVA Tests auf signifikante Aenderungen model_1 vs model_2 (Aenderung signifikant?)
pander::pander(anova(model_1, model_2))| Res.Df | RSS | Df | Sum of Sq | F | Pr(>F) |
|---|---|---|---|---|---|
| 532 | 12023 | NA | NA | NA | NA |
| 531 | 11233 | 1 | 790.6 | 37.37 | 1.893e-09 |
Zum Verständnis dieser Statistik greifen wir kurz zurück auf die verschiedenen Möglichkeiten der Berechnung von Korrelationskoeffizienten zurück. Diese sind:
- Pearson Korrelationskoeffizient (\(r_{xy}\)): entspricht der Kovarianz der \(z\)-transformierten Variablen.
- Partielle Korrealtionskoeffizient (\(r_{xy \cdot z}\)): ist die bivariate Korrelation zweier Variablen, welche mittels linearer Regression vom Einfluss einer Drittvariablen bereinigt wurden.
- Semipartialkorrelation (\(sr_{k \cdot x_j}\)): zwischen Kriterium und dem \(j\)-ten Prädiktor ergibt sich als Korrelation von \(y\) mit dem Residuum \(x_j^*\) der linearen Regression des \(j\)-ten Prädiktors auf den anderen Prädiktor.
Mit anderen Worten, die Semipartialkorrelation gibt den alleinigen Beitrag eines Prädiktors \(x_j\) (bereinigt um die gemeinsamen Anteile mit den restlichen Prädiktoren) am Kriterium an. Das Quadrat dieses Koeffizienten wird unter anderm auch als Nützlichkeit des Prädiktors \(U_k\) bezeichnet und findet sich z.B. in SPSS als \(R^2_{change}\) wieder. Formal:
\(sr_{k \cdot 12 \cdots (k-1)}^2 = R_{y, 12 \cdots k}^2 - R_{y, 12 \cdots k-1}^2\)
Die Berechnung dieser Kennzahlen in R:
# Korrelationen, Paritial- und Semipartialkorrelationen
Korr_Data <- data.frame(wage = M$wage, educ = M$educ, exper = M$exper)
PearsonKorr <- cor(Korr_Data)
ModVgl_Korr <- pander::pander(PearsonKorr)
R2Change_mod_1 <- PearsonKorr[2]^2
# Partial Korrelation zwischen "wage" und "educ" gegeben "exper"
PartKorr_1 <- ppcor::pcor.test(Korr_Data$wage, Korr_Data$educ, Korr_Data$exper)
ModVgl_ParKorr_1 <- pander::pander(PartKorr_1)
# Partial Korrelation zwischen "wage" und "exper" gegeben "educ"
PartKorr_2 <- ppcor::pcor.test(Korr_Data$wage, Korr_Data$exper, Korr_Data$educ)
ModVgl_ParKorr_2 <- pander::pander(PartKorr_2)
# Semi-Partial (part) Korrelation zwischen "wage" und "educ" gegeben "exper"
SemiPartKorr_1 <- ppcor::spcor.test(Korr_Data$wage, Korr_Data$educ, Korr_Data$exper)
ModVgl_SemParKorr_1 <- pander::pander(SemiPartKorr_1)
# Semi-Partial (part) Korrelation zwischen "wage" und "exper" gegeben "edu"
SemiPartKorr_2 <- ppcor::spcor.test(Korr_Data$wage, Korr_Data$exper, Korr_Data$educ)
ModVgl_SemParKorr_1 <- pander::pander(SemiPartKorr_2)
R2Change_mod_2 <- round(SemiPartKorr_2$estimate^2,3)
pander::pander(summary(model_2))| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | -4.904 | 1.219 | -4.024 | 6.564e-05 |
| educ | 0.926 | 0.0814 | 11.37 | 5.563e-27 |
| exper | 0.1051 | 0.0172 | 6.113 | 1.893e-09 |
| Observations | Residual Std. Error | \(R^2\) | Adjusted \(R^2\) |
|---|---|---|---|
| 534 | 4.599 | 0.202 | 0.199 |
Im vorliegenden Beispiel sind daher die beiden Nützlichkeitsmaße \(U_{educ}\) = 0.146 und \(U_{exper}\) = 0.056 von Interesse. Ersteres bedeutet, dass die Varianzaufklärung aufgrund der Verwendung der Variablen educ 14.6% ist. Wird im Modell dann noch der Prädiktor exper aufgenommen, werden zusätzliche 5.6% an Varianz des Kriteriums wage erklärt. Insgesamt werden somit \(R^2 = 0.202\) oder 20.2% der Varianz des Kriteriums erklärt. Der Test (\(t(531) = 11.37, p< .001\)) bestätigt für den Prädiktor educ, sowie (\(t(531) = 6.11, p<.001\)) für den Prädiktor exper die statistische Signifikanz.
Aufgabe MLR 1
Öffne ein neues R-Script und kopiere die bereits bekannte Kopfzeile in diese Datei. Speichere anschließend das Skript unter dem Namen SLR_Aufgabe2.R. Bearbeite nun folgende Aufgabenstellungen:
- Lade die Datei “Album Sales 2.dat”
- erstelle ein lineares Modell zur Vorhersage der Verkaufszahlen (sales) durch die Variable adverts.
- erstelle ein weiteres lineares Modell zur Vorhersage der Verkaufszahlen (sales) durch die Variable adverts, airplay und attract.
- Zeige die Ergebnisse des ersten Modells an.
- Zeige die Ergebnisse des zweiten Modells an.
- Vergleiche die beiden Modelle mit einer ANOVA und interpretiere die Ergebnisse.
- Berechne zur Überprüfung der Multikolinearität den Kennwert Tol und VIF (verwende die Funktion vif(). Hinweis: die Toleranz ist der Kehrwert von VIF)
Wahl relevanter Prädiktoren
Eine wichtige Frage bei der Modellerstellung betrifft die Wahl der besten Prädiktoren. Prinzipiell sollte bereits im Vorfeld der statistischen Analyse bestimmt werden, welche Merkmale für die Modellierung der abhängigen Variablen am geeignetsten sind. Ausreichende theoretische und praktischen Kenntnisse sind daher unbedingt erforderlich. Prädiktoren sind dann gut geeignet, wenn Sie folgende Eigenschaften erfüllen:
- jeder Prädiktor erklärt möglichst viel der Variabilität des Kriteriums (\(|r(y,x_j)| \gg 0\)).
- die Prädiktoren (z.B. \(x_1\) und \(x_2\)) sind im günstigsten Fall voneinander unabhängig (\(r(x_i,x_j) \approx 0\) mit \(i \ne j\)). Korrelieren zwei Prädiktoren mit \(r(x_i, x_j) > 0.8\), kann man schon mit ziemlicher Sicherheit davon ausgehen, dass die Verwendung beider Prädiktoren in einem Modell zu instabilen Regressionskoeffizienten führt und Aussagen zur Schätzung der Regressionskoeffizienten zunehmend ungenau werden (siehe Voraussetzungen der multiplen Regression und Problem der Multikollinearität).
Diese Eigenschaft kann man durch eine einfache paarweise Korrelation prüfen. Vor allem wenn die zweite Eigenschaft nicht gegeben ist, also wenn einen hohe Korrelationen zwischen zwei Prädiktoren vorliegt, wird es bei der Modellierung zu maßgeblichen Problemen (Multikollinearität) kommen (siehe: Voraussetzungen der multiplen Regression.
Neben der Frage nach der Güte einzelner Prädiktoren ist es auch wichtig sich Gedanken über die Anzahl der zu verwendenden Prädiktoren zu machen. Einerseits führt trivialerweise eine höhere Anzahl von Prädiktoren auch zu einer besseren Aufklärung der Varianz im Kriterium. Ausgenommen von Prädiktoren die in keiner Beziehung zum Kriterium stehen, wird jeder zusätzliche Prädiktor mehr oder weniger der verbleibenden Varianz erklären. In den meisten Fällen ist es aber aus zeitlichen/finanziellen oder sonstigen Gründen nicht sinnvoll, eine möglichst große Menge an Prädiktorvariablen zu erheben.
Werden zu viele erklärende Variablen zur Spezifizierung eines Modells verwendet, wird die tatsächliche (geringere) Anpassungsgüte verschleiert. Das Modell wird zwar besser auf die Daten der Stichprobe angepasst, allerdings besteht aufgrund fehlender Generalität keine Übertragbarkeit auf die Grundgesamtheit.
Grundsätzlich sollte wie bereits erwähnt die Wahl der Prädiktoren auf theoretisch und praktisch fundierten Grundlagen erfolgen. Welche der zur Verfügung stehenden Prädiktoren im Endeffekt für das Modell verwendet werden, kann anhand der Modellvergleiche auch im statistischen Sinn evaluiert werden.
Bei der bisher besprochenen Vorgehensweise der Modellerstellung obliegt es dem Analysten, die zu verwendenden Prädiktoren zu bestimmen. Eine weitere Möglichkeit bietet die sogenannte sequentielle Vorgehensweise, bei der die Ein- und Ausschlusskriterien für Prädiktoren durch statistische Kriterien getroffen werden.
Sequentielle Modellbildung
In manchen Fällen sind nicht ausreichende theoretische Grundlagen und Erfahrungswerte bezüglich der Wirksamkeit und Wichtigkeit von Prädiktoren vorhanden. In solchen Fällen kann ein exploratives Vorgehen bei der Modellerstellung sehr hilfreich sein. Die nachfolgend beschriebene sequentielle Modellierung entspricht einem solchen Ansatz.
Bei der sequentiellen Modellbildung wird ein Modell schrittweise mit unabhängigen Variablen erweitert. In der Regel wird jene Variable, die das \(R^2\) am meisten vergrößert (und damit die Vorhersage am meisten verbessert) hinzugefügt.
Abhängig von der Anzahl der verfügbaren Prädiktoren wird die Bildung neuer Modelle entweder abgebrochen, wenn weitere Variablen keinen weiteren statistischen signifikanten Beitrag zur Varianzaufklärung mehr leisten, oder wenn keine weiteren Variablen zur Verfügung stehen.
Aufgrund der statistischen (maschinellen) Entscheidung über die Verwendung von Prädiktoren, wird diese Vorgehensweise vielfach kritisiert. Nehmen wir in einem sehr einfachen Beispiel einmal an, es stehen 2 Prädiktoren (\(x_1, x_2\)) zur Vorhersage der abhängigen Variablen zur Verfügung. Der Prädiktor \(x_1\) klärt geringfügig weniger Varianz des Kriteriums auf als Prädiktor \(x_2\), ersterer ist aber inhaltlich sinnvoller, leichter zu interpretiern und vor allem weit kostengünstiger zu erfassen. Bei der sequentiellen Methode könnte aber aufgrund des Abbruchkriteriums (Signifikanz des Beitrags) genau dieser Prädiktor vom Modell ausgeschlossen werden.
Bei der sequentiellen Methode unterscheidet man noch unterschiedliche Vorgehensweisen hinsichtlich des Hinzufügens/Entfernens von Variablen:
- Vorwärts-Selektion (FORWARD): Die Variablen werden sequenziell in das Modell aufgenommen. Diejenige unabhängige Variable, welche am stärksten mit der abhängigen Variable korreliert wird zuerst zum Modell hinzugefügt. Dann wird jene der verbleibenden Variablen hinzugefügt, die die höchste partielle Korrelation mit der abhängigen Variablen aufweist. Dieser Schritt wird wiederholt, bis sich die Modellgüte (R-Quadrat) nicht weiter signifikant erhöht oder alle Variablen ins Modellaufgenommen worden sind.
- Schrittweise (STEPWISE): Diese Methode ist ähnlich wie “Vorwärts”-Selektion, es wird aber zusätzlich bei jedem Schritt getestet, ob die am wenigsten “nützliche” Variable entfernt werden soll.
- Rückwärts-Elimination (BACKWARD): Zunächst sind alle Variablen im Regressionsmodell enthalten und werden anschließend sequenziell entfernt. Schrittweise wird immer diejenige unabhängige Variable entfernt, welche die kleinste partielle Korrelation mit der abhängigen Variable aufweist, bis entweder keine Variablen mehr im Modell sind oder keine die verwendeten Ausschlusskriterien erfüllen. Im Unterschied zur STEPWISE-Methode wird nicht mehr geprüft, ob die am wenigsten nützliche Variable entfernt werden soll - diese bleibt somit im Modell!
Diese Methoden unterscheiden sich von der sogenannten Einschlussmethode (ENTER), bei der alle Variablen gleichzeitig in das Modell eingefügt werden. Die Enter-Methode wird angewendet, wenn das Modell auf theoretischen Überlegungen basiert. Das heißt, sie eignet sich um Theorien zu testen, während die übrigen Methoden eher im Rahmen explorativer Studien eingesetzt werden können.
Modellvergleiche
Nach einer (explorativen) Analyse der Daten und der Wahl einer passenden Modellklasse, geht es darum, das bestmögliche Modell zu den vorliegenden Daten zu finden. Daher stellt sich die Frage, was “bestmögliches” Modell bedeutet und wie ein solches bestimmt werden kann.
In diesem Zusammenhang wird der Gedanke aufgegriffen, dass mit keinem Regressionsmodell die Realität 1:1 abgebildet werden kann. Nimmt man zu viele erklärende Variablen auf, läuft man in Gefahr das Modell zu “overfitten” (Überanpassung). Ein überangepasstes Modell erklärt die zum Schätzen verwendete abhängige Variable meist sehr gut, schneidet jedoch in der Vorhersage von Daten außerhalb der verwendeten Stichprobe häufig schlecht ab.
Auf der anderen Seite kann ein Modell auch “underfitted” sein, d.h. die aufgenommenen unabhängigen Variablen können die abhängige Variable nur sehr unzureichend erklären.
Modellselektion ist ein allgegenwärtiges Thema in der Statistik/Regressionsanalyse. Dennoch gibt es keine absoluten, objektiven Kriterien anhand derer entschieden werden kann, ob das eine oder das andere Modell gewählt werden sollte. Vielmehr existieren viele verschiedene Verfahren, die versuchen zwischen möglichst viel Erklärungsgehalt des Modells und möglichst wenig Komplexität abzuwägen (siehe dazu Ockhams Rasiermesser) .
In einem Artikel von (Yamashita 2007) wurden folgende Methoden für den Vergleich von Regressionsmodellen untersucht:
- Partial F
- Partial Correlation
- Semi-Partial Correlation
- Akaike Information Criteria (AIC)
Die Autoren schließen aus den Ergebnissen ihrer Untersuchung, dass alle Methoden zu den gleichen Ergebnissen, d.h. zur gleichen Modellentscheidung gelangen. Da aber der AIC einerseits leicht zu interpretieren und andererseits auch auf nichtlineare Modelle und Modelle die auf nicht normalverteilten Daten beruhen zu erweitern ist, wird die Anwendung dieses Kriteriums empfohlen.
Aikaike (AIC)
Das AIC dient also dazu, verschiedene Modellkandidaten zu vergleichen. Dies geschieht anhand des Wertes der log-Likelihood, der umso größer ist, je besser das Modell die abhängige Variable erklärt. Um nicht komplexere Modelle als durchweg besser einzustufen wird neben der log-Likelihood noch die Anzahl der geschätzten Parameter als Strafterm mitaufgenommen.
\[\begin{equation} AIC_k = 2 \cdot |k| - 2\cdot \hat{L}_k \tag{4} \end{equation}\]
In der Formel steht \(k\) für die Anzahl der im Modell enthaltenen Parameter und \(\hat{L}_k\) für den Wert der log-Likelihoodfunktion. Gemäß dem Eigenschaften dieser Kennzahl wird also jenes Modell \(k\) gewählt, welche den kleinsten AIC aufweist.
Das AIC darf nicht als absolutes Gütemaß verstanden werden. Auch das Modell, welches vom Akaike Kriterium als bestes ausgewiesen wird, kann eine sehr schlechte Anpassung an die Daten aufweisen. Die Anpassung ist lediglich besser als in den Alternativmodellen. Die praktische Bedeutung soll anhand eines einfachen Beispiels und der Verwendung des Kriteriums bei unseren Beispieldaten erläutert werden.
Nehmen wir an, dass drei Modellvergleiche (\(mod_1\), \(mod_2\), \(mod_3\)) folgende AIC-Werte ergeben haben:
\(AIC_1 = 100, AIC_2 = 102, AIC_3 = 110\). Berechnet man \(e^{(AIC_{min} - AIC_i)/2}\), kann das Ergebnis folgendermaßen interpretiert werden:
- Beim \(mod_2\) ist es um das \(e^{(100-102)/2} = 0.368\)-fache wahrscheinlicher den Informationsverlust zu verringern als bei Modell 1 (\(mod_1\)).
- Beim \(mod_3\) ist es um das \(e^{(100-110)/2} = 0.007\)-fache wahrscheinlicher den Informationsverlust zu verringern als bei Modell 1 (\(mod_1\)).
Bei diesem Beispiel würde man also \(mod_3\) für weitere Betrachtungen ausschließen. Nachdem aber die Modelle \(mod_1\) und \(mod_2\) sehr nahe beisammen liegen, ist es mit den vorliegenden Daten nicht möglich, eine klare Entscheidung für eines der beiden Modelle zu treffen.
Man könnte durchaus noch zusätzliche Daten erheben um dadurch eventuell eine klarere Trennung der beiden Modelle (\(mod_1\), \(mod_2\)) zu erkennen. Ist das nicht möglich, könnte man beide Modelle mit der relativen likelihood gewichten und auf eine statistische Signifikanz testen, oder davon ausgehen, dass mit den vorliegenden Daten eine Modellwahl eben nicht eindeutig zu treffen ist.
Kreuzvalidierung
Die Vorhergehensweise bei der Kreuzvalidierung ist relativ simpel:
- Erstelle ein/mehrere Modell(e) und berechne die jeweiligen Modellparameter \(b_i^j\) (mit \(j = j\)-tes Modell und \(i = i\)’ter Parameter) mit einer Teilmenge der zur Verfügung stehenden Daten (z.B. Training_Data \(\subset\) DF).
- Verwende die restlichen Daten um mit den entsprechenden Modellen Vorhersagen zu berechnen.
- Berechne die Differenz der beobachteten Daten und der vorhergesagten Daten. Diese Differenz entspricht dem Fehler des Modells (\(\rightarrow \epsilon_i\)).
- Berechne den mittleren quadratischen Fehler der Differenzen.
Im nachfolgenden Beispiel soll die Berechnung/Durchführung des AIC und der Kreuzvalidierung anhand simulierter Daten gezeigt und diskutiert werden.
AIC und Kreuzvalidierung in R
Kopier den nachfolgenden Code in dein R-Script und führe diesen Zeilenweise aus.
# AIC & BIC vs. Crossvalidation
# https://www.r-bloggers.com/aic-bic-vs-crossvalidation/
# Erzeuge einen Praediktor (gleichverteilt zwischen -2 und +2)
x <- runif(100,-2,2)
# Erzeuge ein Kriterium (Polynom dritter Ordnung mit zufalligen, normalverteilten Noise)
y <- 2*x^3 + x^2 - 2*x +5 + rnorm(100)
xy <- data.frame(x=x, y=y)
# Definiere das Maximum fuer des Polynoms mit dem die Daten
# modelliert werden sollten.
MaxPoly <- 5
# Erzeuge einen Datenframe in welche die Modellvorhersagen gespeichert werden.
x.new <- seq(min(x), max(x), by=0.1)
degree <- rep(1:MaxPoly, each=length(x.new))
predicted <- numeric(length(x.new)*MaxPoly)
new.dat <- data.frame(x=rep(x.new, times=MaxPoly),
degree,
predicted)
# MODELLANPASSUNG durch Polynome der Ordnung 1 (linear) bis 7
for(i in 1:MaxPoly){
model <- lm(y ~ poly(x, i))
new.dat[new.dat$degree==i,3] <- predict(model,
newdata = data.frame(x = x.new))
}
# Daten und angepasste Modelle anzeigen
p <- ggplot() +
geom_point(aes(x, y), xy, colour="blue") +
geom_line(aes(x, predicted, colour=as.character(degree)), new.dat) +
scale_colour_discrete(name = "Degree") +
theme_bw()
print(p, comment = FALSE)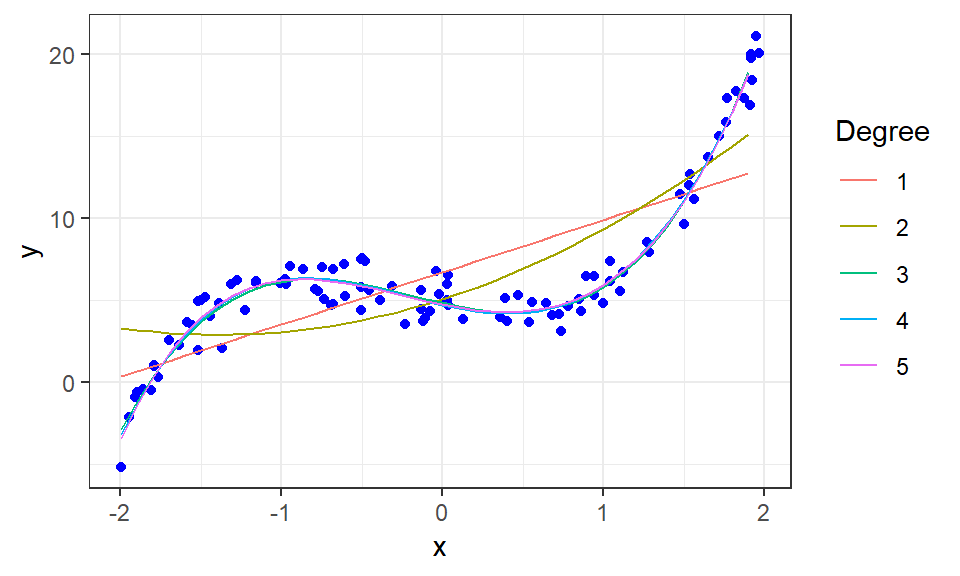
# Leeren Datenframe fuer Speichern aller AIC und BIC Werte aller Modelle erzeugen
AIC.BIC <- data.frame(criterion = c(rep("AIC",MaxPoly),
rep("BIC",MaxPoly)),
value = numeric(MaxPoly*2),
degree = rep(1:MaxPoly, times=2))
# Berechnen von AIC/BIC fuer jedes Modell
for(i in 1:MaxPoly)
{
AIC.BIC[i,2] <- AIC(lm(y~poly(x,i)))
AIC.BIC[i+MaxPoly,2] <- BIC(lm(y~poly(x,i)))
}
# FUNKTION zur Kreuzvalidierung mit "leave one out" fuer y ~ poly(x, degree) Polynome
crossvalidate <- function(x, y, degree)
{
preds <- numeric(length(x))
for(i in 1:length(x))
{
x.in <- x[-i]
x.out <- x[i]
y.in <- y[-i]
y.out <- x[i]
m <- lm(y.in ~ poly(x.in, degree=degree) )
new <- data.frame(x.in = seq(-3, 3, by=0.1))
preds[i] <- predict(m, newdata=data.frame(x.in=x.out))
}
# Berechnen des quadratischen Fehlers
return(sum((y - preds)^2))
}
# Kreuzvalidierung und Speichern der quadratischen Fehler aller Modelle
a <- data.frame(cross=numeric(MaxPoly))
for(i in 1:MaxPoly)
{
a[i,1] <- crossvalidate(x, y, degree=i)
}
# Anzeige der AIC gegen die Modlellkomplexitaet (= Grad des Ploynoms)
AIC.plot <- qplot(degree,
value,
data=AIC.BIC,
geom="line",
linetype=criterion) +
xlab("Grad des Polynoms") +
ylab("Abhaengie Variablenwerte") +
labs(title="Informationstheory & Bayes") +
geom_segment(aes(x=3, y=400, xend=3, yend=325),
arrow = arrow(length = unit(0.3, "cm"),
angle=20,
type="closed")) +
theme(legend.position=c(0.8,0.5)) +
theme_bw()
print(AIC.plot, comment = FALSE)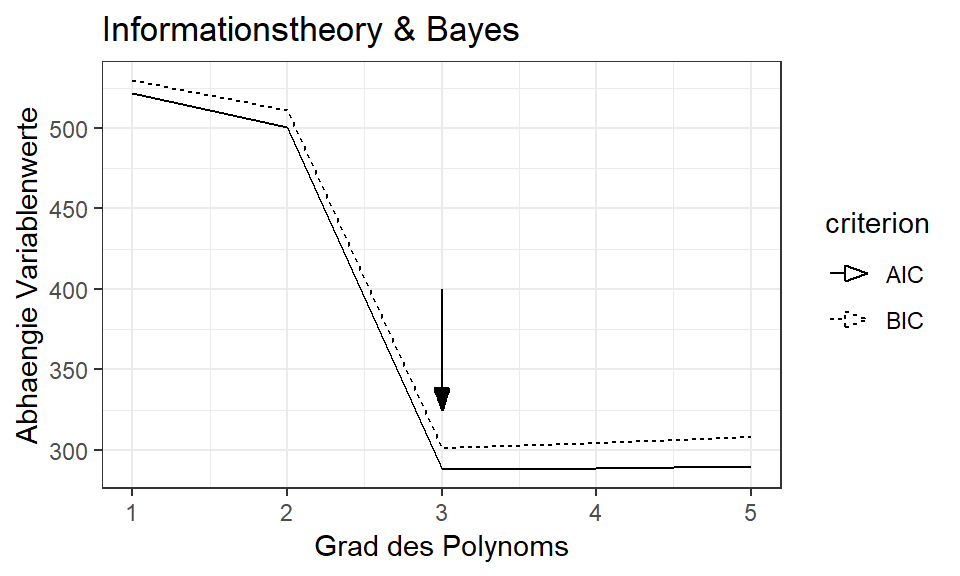
# Anzeige der Kreuvalidierten quadratischen Fehler gegen die Modelllkomplexitaet
# (Modellkomplexitaet = Grad des Polynoms)
cross.plot <- qplot(1:MaxPoly, cross, data=a, geom=c("line")) +
xlab("Grad des Polynom") +
ylab("Quadratischer Fehler") +
geom_segment(aes(x = 3, y = 400, xend = 3, yend = 200),
arrow = arrow(length = unit(0.3, "cm"),
angle = 20, type="closed")) +
labs(title="Kreuzvalidierung") +
theme_bw()
print(cross.plot, comment = FALSE) 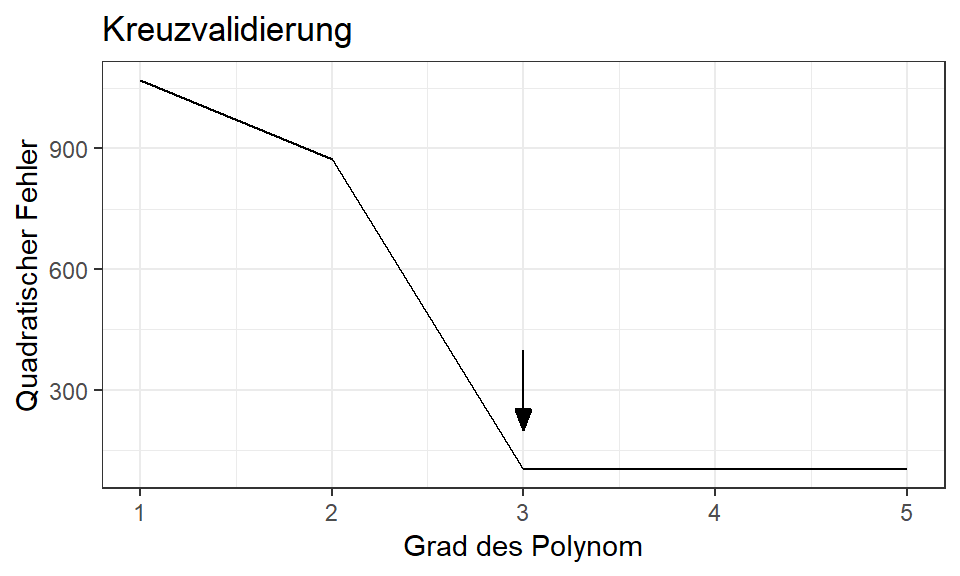
Voraussetzungen MLR
Folgende Voraussetzungen müssen/sollten bei der linearen Modellierung mit mehreren Prädiktoren erfüllt sein, damit die Ergebnisse auch sinnvoll interpretiert werden können (Bemerkung: im folgenden sei die abhängige Variable \(y\) und die Prädiktoren mit den Zahlen \({1, 2, \cdots, k}\) bezeichnet):
- Lineare Beziehung zwischen den Variablen (keine Ausreißer): eine einfache Prüfung erfolgt visuell mit Streudiagrammen, wobei alle Beziehungen, also \(r_{y\cdot1}, r_{y\cdot2}, \cdots, r_{y\cdot k}, \cdots, r_{1\cdot2}, r_{1\cdot k}, \cdots, r_{(k-1)\cdot k}\) zu betrachten sind!
- Varianzgleichheit der Residuen (Homoskädasdizität): auch diese Vorausstung kann visuell geprüft werden. Dabei wird ein Streudiagramm der Residuen erstellt, in welchem auf der x-Achse die standardisierten vorhergesagten Werte und auf der y-Achse doe standardisierten Residuen aufgetragen werden. Heteroskedastizität liegt vor, wenn die Punktewolke nicht gleichverteilt um die Gerade liegen!
Abbildung 14: Homoskedastizität vs. Heteroskedastizität
Bekannte Verfahren, um die Nullhypothese „Homoskedastizität“ zu überprüfen sind der:
* Levene-Test
* Goldfeld-Quandt-Test
* White-Test
* Glejser-Test
* RESET-Test
* Breusch-Pagan-Test- Normalverteilung der Residuen: mittels Histogramm der Fehler zu prüfen - sollte halbwegs normalverteilt sein mit einem Erwartungswert des Fehlers \(E(\varepsilon) = 0\).
Unabhängigkeit der Residuen (keine Autokorrelation): verletzt wird diese Voraussetzung, wenn aufeinanderfolgende Werte abhängig sind (z.B. auf einen hohen Wert folgt ein hoher Wert, etc.). Vor allem bei Längsschnittdaten ein Thema, bei welchen die Prüfung durch die Durbin-Watson-Methode empfohlen wird. Es gilt: \(d = \frac{\sum_{i} (e_i - e_{i-1})^2}{\sum_{i} (e_i)^2}\) mit \(d \approx 2\), Werte zwischen \(1.5 < d < 2.5\) sind noch akzeptabel.
- Vollständig spezifizierte Modelle: werden maßgebliche Prädiktoren nicht im Modell berücksichtigt, wird es auch kaum gelingen, die Varianz des Kriteriums zufriedenstellend zu erklären. Andererseits bewirken Modelle mit vielen Prädiktoren, dass die \(\beta\)-Gewichte entsprechend klein werden. Bei derartigen Gegebenheiten ist die Stichprobe entsprechend groß zu wählen.
Keine Multikollinearität: Multikollinearität bedeutet, dass Prädiktoren existieren, die hoch miteinander korrelieren (z.B. \(r_{1\cdot2} > 0.8\)). Damit wird es für das Modell schwer, den jeweiligen Beitrag den Prädiktoren zuzuordnen. Besteht rein das Interesse an maximaler Varianzaufklärung des Kriteriums, ist eine hohe Multikollinearität zu vernachlässigen - die \(\beta\)-Gewichte der einzelnen Prädiktoren darf man dann allerdings nicht interpretieren. Spielen jedoch gerade diese eine wichtige Rolle, kann man entweder hoch korrelierte Prädiktoren zusammenfassen (eventuell Faktorenanalyse/Clusteranalyse vorher durchführen), oder entsprechende Prädiktoren ausschließen. Allerdings sollte man vor dem Ausschluss von Prädiktoren diese auf eventuelle Suppressionseffekte prüfen.
- Negative und reziproke Suppression: man spricht von Suppressionseffekten, wenn ein Prädiktor aus einem anderen Prädiktor irrelevante Varianz unterdrückt (suppression) und dadurch die Beziehung zwischen diesem Prädiktor und dem Kriterium erhöht. Solche Effekte können durchaus beträchtlich sein und u.U. auch einen Prädiktor, der nichts mit dem Kriterium an sich zu tun hat (\(r_{y\cdot k} \approx 0\)), als wichtigen Bestandteil des Modells werden lassen. Die Aufnahme des Suppressors in das Regressionsmodell hat somit den Effekt, den anderen Prädiktor von diesen Fehlereinflüssen zu bereinigen. Erkennbar sind Suppressionseffekte einerseits durch Vorzeichenwechsel bei Korrelationen (Nullter Ordnung, also der Produkt-Moment-Korrelation) vs. \(\beta\)-Gewichten (negative Suppression, bzw. NET-Suppression). D.h., dass für nicht-negative Validitäten8 ist der Prädiktor \(2\) ein negativer Suppressor, falls seine partielle Steigung negativ ist, d. h., falls \(B_2 < 0\). Eine reziproke Suppression liegt vor, wenn für nicht-negative Validitäten die Korrelation der Prädiktoren negativ ist, d. h., falls \(r_{1\cdot2} < 0\). Weitere Details zu Suppressionseffekten siehe Literatur und Diskriminanzanalyse.
- Hohe Reliabilität der Prädiktoren und des Kriteriums: Variablen sind hochreliabel, wenn sie weitgehend frei von Zufallsfehlern sind, also bei Messwiederholung ähnliche Ergebnisse liefern.
- Keine Varianzeinschränkung: eine Einschränkung führt i.A. zu eingeschränkten (niedrigeren) Korrelationen. Z.B.: aus 500 Personen werden 100 augrund eines Aufnahmeverfahrens zu einem Studium zugelassen. Will man die Validität des Aufnahmeverfahrens anhand der Beziehung Studienerfolg und Leistung beim Aufnahmetest prüfen, wird es aufgrund der eingeschränkten Variabilität durch die Aufnahmekriterium zu einer Unterschätzung kommen.
- Unabgängigkeit der Beobachtungseinheiten: eine Verletzung dieser Voraussetzung, kann zu einer maßgeblichen Reduktion der Teststärke des Modells führen. Z.B. soll die Teamorientierung in einem Unternehmen untersucht werden. Diese wird sicher zwischen den einzelnen Personen variieren, aber darüber hinaus kann diese auch abhängig von der Abteilung sein, in welcher Personen arbeiten. Die Variabilität kann dadurch bei bestimmten Abteilungen stark eingeschränkt sein, was einer Reduktion des Stichprobenumfangs und damit einer Teststärkenreduktion gleichzusetzen ist. In solchen Fällen könnte man eine Multilevel-Analyse (gemischtes hierarchisches Modell) einsetzen!
Zusammenfassend lässt sich festhalten, dass eine Verletzung einer/mehrerer dieser Voraussetzungen meistens dazu führt, dass die Genauigkeit der Vorhersage gemindert wird. Relativ einfach zu prüfen sind die ersten drei Voraussetzungen (graphisch, Kennwerte wie Korrelation, etc.). Bei der Überprüfung der restlichen Voraussetzung muss man i.A. auf entsprechende statische Verfahren zurückgreifen, die hier aber nicht näher besprochen werden. Einen Überblick über die Möglichkeiten zur Überprüfung der Voraussetzungen finden Sie z.B. unter (UZH 2018), oder MR2 - (Hemmerich 2018).
Referenzen
Yamashita, T. 2007. “A Stepwise Aic Method for Variable Selection in Linear Regression.” Communications in Statistics Theory and Methods, No. 36:13:2395–2403. https://doi.org/10.1080/03610920701215639.
UZH. 2018. “Multiple Regressionsanalyse.” https://www.methodenberatung.uzh.ch/de/datenanalyse_spss/zusammenhaenge/mreg.html.
Hemmerich, W. A. 2018. “StatistikGuru Multiple Lineare Regression in Spss, Version 1.96.” https://statistikguru.de/spss/multiple-lineare-regression/einleitung-2.html.
Die Korrelationen des Kriteriums mit den Prädiktorvariablen bezeichnen wir als Validitäten, d. h. die Validität der \(j\)-ten Prädiktorvariablen ist gleich ihrer Korrelation mit dem Kriterium.↩