Variabilität
Bevor wir uns mit einzelnen Techniken und Verfahren der linearen Modellbildung auseinandersetzen, soll in einem kurzen Exkurs eines der grundlegensten Prinzipien der statistischen Modellbildung wiederholt und diskutiert werden - die Varianz von beobachten Werten.
Eigentlich ist es die Variabilität von Merkmalen, die statistische Methoden für die Erklärung von Effekten überhaupt erst auf den Plan ruft. Würden Merkmale wie z.B. Leistung einer Person, Persönlichkeitsmerkmale, Wetter, Produktionsgenauigkeit etc. nicht schwanken/variieren, würden wir heute nicht in diesem Raum sitzen und uns mit statistischen Modellen beschäftigen.
Der Begriff Variabilität ist für uns so alltäglich, dass wir ganz selbstverständlich damit umgehen. Doch was steckt wirklich dahinter? Wie können wir Sie nutzen um komplexere Eigenschaften einer Sache oder eines unerklärlichen Phenomäns auf die Spur zu kommen?
Betrachten wir zunächst einmal ein sehr einfaches Beispiel. In den nachfolgenden Graphen sind (sehr vereinfacht) mehrere Möglichkeiten dargestellt, wie eine Person mitsamt Hund sich entlang einer Straße bewegt.
Abbildung 1: Gassi gehen mit Blindenhund. Die blaue Linie beschreibt den Weg des Hundehalters, die Orange den des Hundes. Die Grüne Line ist die Referenzlinie, von welcher aus der Abstand zur jeweiligen Position (Hund und Mensch) zu sechs Beobachtungszeitpunkten gemessen wurde.
Die Daten der Messungen sind in folgender Tabelle gegeben:
| Mensch | Hund | MenschD | HundD | KP | ZMensch | ZHund | ZKP |
|---|---|---|---|---|---|---|---|
| 4 | 3 | 0.83 | 1 | 0.83 | 0.71 | 0.71 | 0.5 |
| 5 | 4 | 1.83 | 2 | 3.66 | 1.56 | 1.42 | 2.22 |
| 2 | 1 | -1.17 | -1 | 1.17 | -1 | -0.71 | 0.71 |
| 3 | 2 | -0.17 | 0 | 0 | -0.15 | 0 | 0 |
| 2 | 0 | -1.17 | -2 | 2.34 | -1 | -1.42 | 1.42 |
| 3 | 2 | -0.17 | 0 | 0 | -0.15 | 0 | 0 |
- In obiger Tabelle zeigen die Spalten Mensch und Hund jeweils den Abstand zur gedachten Beobachtungslinie pro Beobachtungszeitpunkt.
- Die Spalten MenschD und HundD ist jeweils die Differenz jeder Beobachtung zum jeweiligen Mittelwert aller Beobachtungen, also \(MD_i = M_i - \bar{M}\) und \(HD_i = H_i - \bar{H}\) mit \(i \in \{1,6\}\).
- Die Spalte KP zeigt das Kreuzprodukt, also \(KP_i = MD_i \cdot HD_i\) mit \(i \in \{1,6\}\).
- Die Spalten ZMensch und ZHund entsprechen den \(z\)-transformierten Werten, also \(z_i^M = (M_i - \bar{M}) / sd(M)\) und \(z_i^H = (H_i - \bar{H}) / sd(H)\)) mit \(i \in \{1,6\}\).
- Die Spalte ZKP entspricht dem Kreuzprodukt der z-Transformierten Werte, also \(ZKP_i = ZM_i \cdot ZH_i\) mit \(i \in \{1,6\}\).
Statistische Kennwerte für obige Daten (Mittelwert, Varianz und Standardabweichung) sind in folgender Tabelle dargestellt:
| Mensch | Hund | MenschD | HundD | KP | ZMensch | ZHund | ZKP | |
|---|---|---|---|---|---|---|---|---|
| Mean | 3.167 | 2 | -0.003 | 0 | 1.333 | -0.005 | 0 | 0.808 |
| Var | 1.367 | 2 | 1.367 | 2 | 2.052 | 0.997 | 1.008 | 0.756 |
| SD | 1.169 | 1.414 | 1.169 | 1.414 | 1.433 | 0.998 | 1.004 | 0.869 |
Wenn also ein Hund jeder Bewegung der Person folgt und dabei auch stets denselben Abstand hält, sind deren beobachteten Pfade zwar örtlich gesehen unterschiedlich, aber die Varianz des einen erklärt vollständig die Varianz des anderen Pfades. Mit anderen Worten, die beiden Pfade zeigen eine perfekte Kovariation. Formal wird diese Kovariation als durchschnittliche Summe der Kreuzprodukte ermittelt, also (M = Mensch, H = Hund):
\(cov(M, H) = \frac{\sum_{i=1}^{6} (M_i - \bar{M}) \cdot (H_i - \bar{H})}{N-1} = 1.60\)
Setzt man die Beispieldaten in diese Berechnungsvorschrift ein, erhält man für die Summe der Kreuzprodukte 8. Die Kovarianz der beobachteten Werte ist (als durchschnittliche Kreuzproduktsumme) somit \(cov(M,H) =\) 1.6. Die Korrelation berechnet sich dann ganz einfach zu:
\(r(M, H) = \frac{cov(M,H)}{s_M \cdot s_H} = \frac{1.6}{1.169 \cdot 1.414} = 0.968 \simeq 1\)
Im vorliegenden Beispiel ergibt sich eine Korrelation \(r(M,H) =\) 0.97 (also eine positive und perfekte Korrelation).
Der Korrelationskoeffizient hat gegebüber der Kovarianz den Vorteil, dass er durch die Normierung über die Standardabweichungen:
- einen (einheitenlosen) Wertebereich zwischen \(r \in [-1, 1]\) aufweist und damit vergleichbar mit anderen Korrelationswerten wird.
- Als praktische Effektgröße interpretiert werden kann.
- Das Quadrat des Korrelationskoeffizienten (\(r^2\), auch Varianzaufklärung, Determinationskoeffizient genannt) Auskunft über die aufgeklärte Varianz gibt.
Letzteres Maß spielt eine wesentliche Rolle sowohl bei der Korrelationsanalyse, als auch bei der multiplen Regression und anderen Verfahren.
Die Bedeutung der Kovarianu sei anhand des verwendeten Beispiels nochmals verdeutlicht:
Im Fall einer perfekten Kovarianz (also 100% Übereinstimmung der Bewegungen von Mensch und Hund), braucht man nur mehr die Bewegung einer Variablen zu wissen (z.B. die des Menschen), um die Bewegungen des Hundes zu bestimmen (erklären). Somit erklärt die Variabilität der Bewegung vom Menschen zu 100 % die Variabilität der Bewegungen des Hundes.
Die Beziehung zwischen zwei (intervallskallierten) Variablen lässt sich am besten mit einem Streudiagramm darstellen:
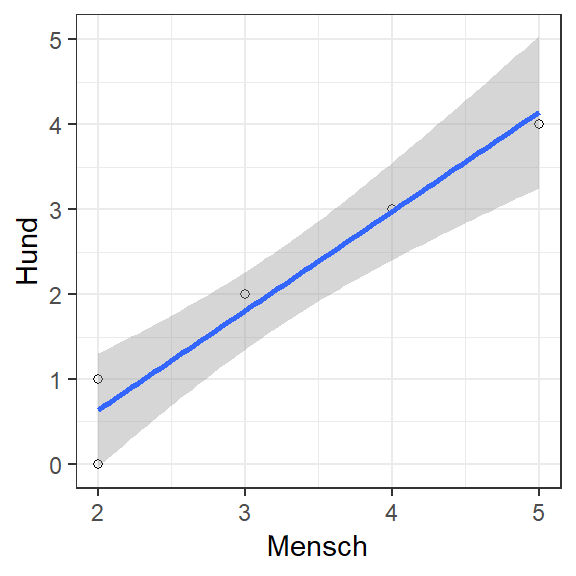
Die folgende Abbildung zeigt ein weiteres Mensch-Hund Beispiel:
Abbildung 2: in diesem Beispiel scheint es sich um eine Hund zu handeln, der bestmöglich das Gegenteil vom Menschen macht. Bestmöglich dahingehen, dass er nicht nur in die genau entgegengesetzte Richtung ausweicht, sondern dabei auch auf den genauen Abstand der Abweichung achtet.
In diesem Fall ist die Korrelation auch perfekt, nur eben in die entgegengesetzte Richtung, was zur Folge hat, dass diese Korrelation den Wert \(r(M,H) = -1\) zeigt.
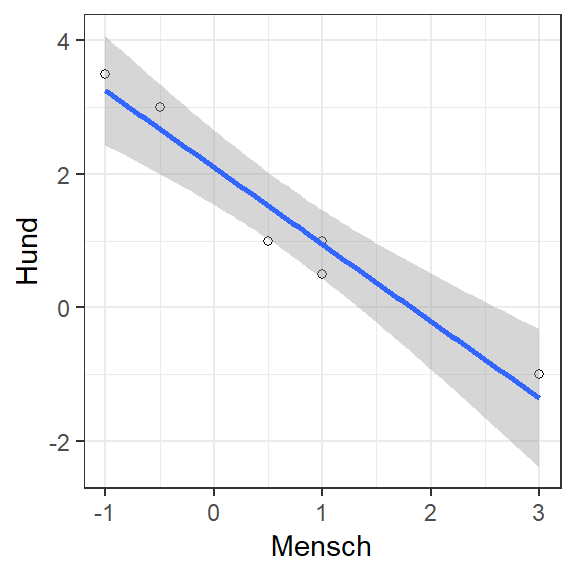
Interessant und der Praxis am ehesten entsprechend, sind jedoch Fälle, in denen zwei Variablen nur teilweise Gemeinsamkeiten aufweisen. Im folgenden Beispiel wäre
![Abbildung 3: Hund und Mensch bewegen sich zum Teil unabhängig, zum Teil aber auch synchron. Dies entspricht dann einer Kovarianz, bzw. Korrelation die irgendwo zwischen r \in [-1, 1] liegt (im Beispiel ist r(M,H) = 0.5 und somit r^2 = 0.25).](Images/GassiBeliebigeKorrelation.JPG)
Abbildung 3: Hund und Mensch bewegen sich zum Teil unabhängig, zum Teil aber auch synchron. Dies entspricht dann einer Kovarianz, bzw. Korrelation die irgendwo zwischen \(r \in [-1, 1]\) liegt (im Beispiel ist \(r(M,H) = 0.5\) und somit \(r^2 = 0.25\)).
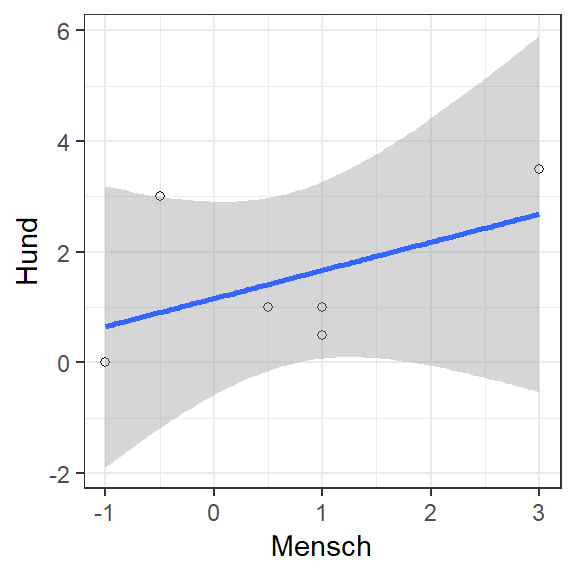
Die Korrelation liegt in diesem Beispiel bei \(r(M,H) = 0.5\). Daraus lässt sich auch nochmals eine sehr wichtige Erkenntnis bezüglich der geteilten Varianz der beiden Variablen festhalten:
Bei einer Korrelation von \(r(x,y) = 0.5\) entspricht der Determinationskoeffizient \(r^2(x,y) = 0.25\). In Prozent ausgedrückt, werden als 25% der Variabilität einer Variablen (z.B. Hund) durch die Variable Mensch erklärt. In welchen Abschnitten der Daten diese gemeinsame Variablität auftritt, lässt sich durch den \(r\) nicht bestimmen.
Diese Feststellung führt uns aber zu einer weiteren Betrachtung von Variablitäten:
Abbildung 4: Hund und Mensch scheinen sich wieder synchron, aber in gegenseitiger Richtung zu bewegen. Man würde also eine negative und hohe Korrelation erwarten. Interressant ist jedoch die Beobachtung, dass ein Versatz der Beobachtungen um eine Einheit zu einem hohen positiven Zusammenhang führen würde!
Würde man davon ausgehen, dass sich der Mensch und Hund bei jedem Messzeitpunkt (1 bis 6) jeweils auf der gleichen Höhe befunden haben, dann wird man eine hohe negative Korrelation erhalten. Nimmt man jedoch an, dass der Mensch zum Messzeitpunkt (MZP) 1, der Hund aber bereits auf MZP 2 war, dann verschiebt sich die Spur des Hundes einfach um einen MZP nach oben! Korreliert man nun diese beiden Beobachtungen, würde sich eine nahezu perfekte positive Korrelation ergeben!
Durch schrittweises Verschieben der Werte einer Variablen um eine Einheit (\(\tau_i\)) mit anschließender Berechnung der Korrelationskoeffizienten (\(r_{\tau_i}(x,y)\)), erhält man in Abhängigkeit von der Anzahl der Verschiebungen (\(i \in [0, N-1]\)) maximal \(N\) neue Korrelatinskoeffizienten. Man bezeichnet diese Art der Korrelationsberechnung als Kreuzkorrelation.
Für das Beispiel ergibt sich eine normale Korrelation von \(r(M,H)=\) -1. Die Korrelationen berechnet nach dem Versatzprinzip ergeben folgendes Bild:
Die Verschiebung \(\tau\) wurde in diesem Beispiel mit \(i = 4\) angegeben, d.h. es wurden die Werte der Variablen Hund um jeweils vier Schritte nach links und vier Schritte nach rechts verschoben. Bei jeder Verschiebung wurde die Korrelation berechnet (im Graphen ist die Verschiebung mit Lag auf der x-Achse angegeben). Auf der y-Achse wird der entsprechende Korrelationskoeffient angezeigt.
| Tau | CrossCorr |
|---|---|
| -4 | -0.4253 |
| -3 | 0.431 |
| -2 | -0.3678 |
| -1 | 0.6609 |
| 0 | -1 |
| 1 | 0.6609 |
| 2 | -0.3678 |
| 3 | 0.431 |
| 4 | -0.4253 |
Die Werte der Tabelle zeigen nochmals den krassen Wechsel der Korrelation zwischen den Werte \(\tau = 0\) (also keiner Verschiebung) und \(\tau = 1\). Werden die Werte um nur einen Beobachtungspunkt verschoben, ändert sich die Korrelation von einer perfekt negativen, zu einer sehr hohen positiven Korrelation!
Eine weitere wichtige Eigenschaft die mit Hilfe dieser Vorgehensweise geprüft werden kann, ist die der sogenannten Autokorrelation. Diese funktioniert im Prinzip wie die eben beschriebene Kreuzkorrelation, mit dem Unterschied, dass eine Variable mit verschobenen “Eigenversionen” korreliert wird. Folgendes Beispiel zeigt das Ergebnis für die Variable Mensch unseres Beispiels:
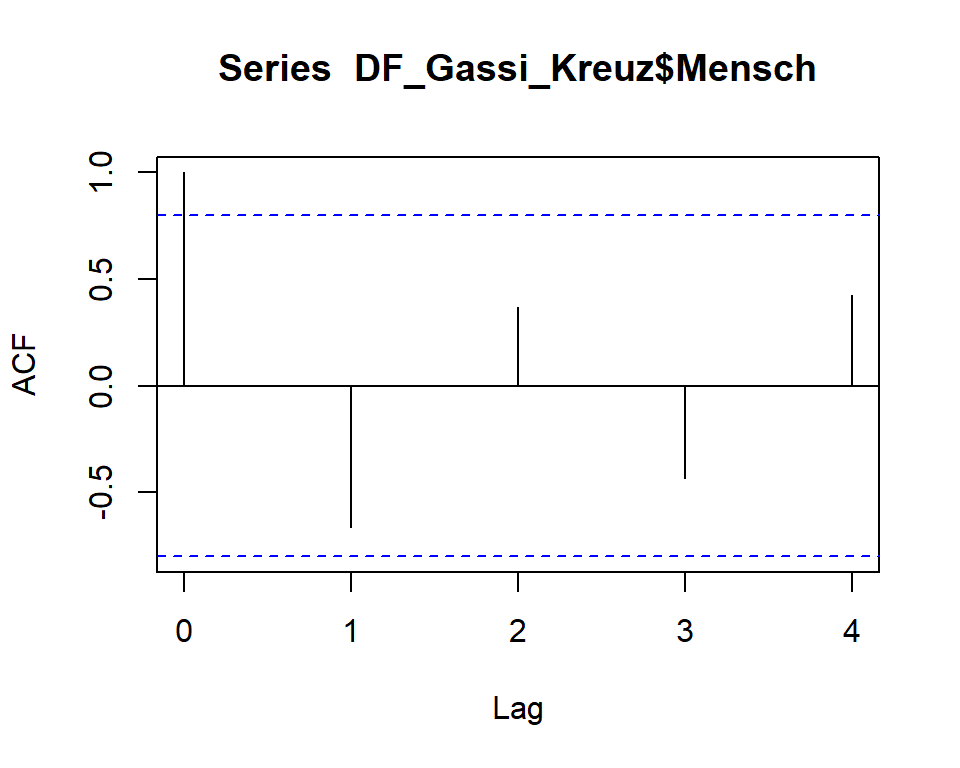
Die Verschiebung \(\tau\) wurde in diesem Beispiel mit \(i = 4\) angegeben, d.h. es wurden die Werte der Variablen Mensch ebenfalls schrittweise in eine Richtung verschoben. Bei jeder Verschiebung wurde die Korrelation berechnet (im Graphen ist die Verschiebung mit Lag auf der \(x\)-Achse angegeben). Auf der \(y\)-Achse wird der entsprechende Korrelationskoeffient angezeigt.
| Tau | CrossCorr |
|---|---|
| 0 | 1 |
| 1 | -0.6609 |
| 2 | 0.3678 |
| 3 | -0.431 |
| 4 | 0.4253 |
Die perfekte positive Korrelation bei einer Verschiebung um den Wert \(\tau = 0\) ist bei der Autokorrelation trivial, da es sich ja um einen direkten Vergleich der Variablen mit sich selbst handelt. Bei Lag = 1 wird jedoch ersichtlich, dass sich die Korrelation ändert (auf \(r = -0.66\)), springt dann wieder auf \(r = +0.37\) usw.
Es ist zu beachten, dass dieser Datensatz nur zu Demonstrationszwecken erzeugt wurde. Eine inhaltliche Interpretation wäre im gegebenen Fall nicht angebracht.
Nichts desto trotz sollte durch diese Beispiel gezeigt werden, dass sowohl die Kreuzkorrelation als auch die Autokorrelation vor allem in der Zeitreihenanalyse (und damit auch bei Längsschnittstudien) wichtige Erkenntnisse über die betrachteten Variablen liefern können. Vor allem kann eine vorliegende Autokorrelation bei der MLR zu beträchtlichen Einschränkungen der Gültigkeit einen Modells beitragen. Bei den MLR-Methoden werden wir noch über Möglichkeiten sprechen, Autokorrelationen auf statitische Signifikanz zu prüfen (Stichwort: Durbin-Watson).